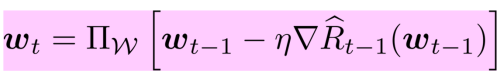Sen(Qian)’s Memo

教科書ではないけど、いくつかのスライドで勉強する。

英語のPDFのスライド

日本語のPDFの解説

ずばり、訓練データの分布とテストデータの分布が違うということ。

以下のような細分ができる。

それぞれの例を挙げてみる。

• Covariance Shift　TrainとTestの間のサンプルの分布が違うが、ラベルの分布が同じ。白黒画像とカラー画像の例。
• Label Shift　　ラベルの分布が違う場合。同じサンプル分布でもラベル付けの方法が変わった場合。
• Output Noise　　TrainとTestの間で、各サンプルについての出力結果が変わる問題。　ノイズが入るとか。
• Class-conditional Shift　　同じラベルの持つデータの分布が異なる。

Joint Shift + Label Shiftなどのように複数兼ね持つ場合がある。

Covariance Shiftを持つが、Output Noiseは持たないもの。

車の写真を見せれば正解は車、猫の写真を見せれば正解は猫でそのままであるが、訓練データがモノクロでテストデータがカラーである場合など。

解決法としては、Importance-Weighted Trainingである。普通の訓練は左、改善後は右。

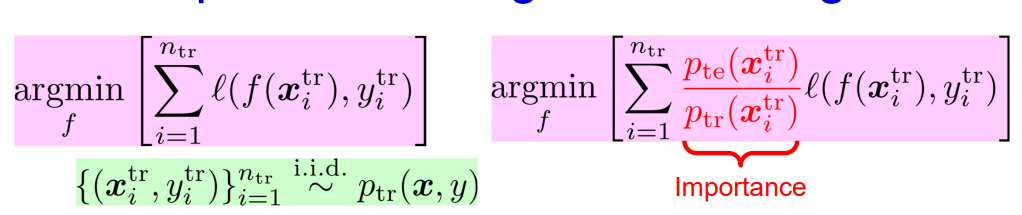
左は$p_{tr}(\mathbf{x}^{tr}) / p_{tr}(\mathbf{x}^{tr}) = 1$であるとみなせば、右は分子を$p_{tr}(\mathbf{x}^{tr}) \to p_{te}(\mathbf{x}^{tr})$のように変えている。

分子だけで十分では？と思えてくるけど左は何もない1である以上、比率で計算するべきである。

これを利用して、$p_{te}$からサンプリングが難しいとき、密度比がわかれば$p_{tr}$がわかるなら逆算ができるという手法である。

では、どのようにImportance=密度比を推定するのか？

ここで、$r(\mathbf{x}) = p_{te}(\mathbf{x}) / p_{tr}(\mathbf{x})$とする。$p_{te}(\mathbf{x})$と$r(\mathbf{x}) p_{tr}(\mathbf{x})$の分布を一致させたい。

具体的には以下のようなものである。

これだけでは不十分である。N次の積率=モーメントは$\mathbb{E}[X^N]$であり、無限次元まで考えてすべてを考えて一致させないと分布は一致しない。

一次モーメントは平均、二次モーメントは分散、三次モーメントは歪度、四次モーメントは尖度。

すべての次元を捉えるため、$\exp$はテイラー展開すると無限次元展開できることを利用して、ガウシアンカーネルを使えばよい。これは再生核ヒルベルト空間$\mathcal{H}$を定義してそれを使えばいい。カーネル関数はガウシアンカーネルを使う。

ここでの再生核ヒルベルト空間は1引数をとる関数の間の内積を定義している空間であり、その内積の計算方法がガウシアンカーネルである。

以下のように最小二乗法で推定する。

これは、Bergman Divergenceに拡張することもできる。

Bergman Divergenceとは以下のように2点$p, q$の距離を測る手法である。$\phi$は凸関数。このDivergenceは交換則が成り立たず、一般的なDivergenceの一般化である。

つまり、二乗誤差を任意のDivergenceに置き換えてもいい。

1. まずは上記の手法のように、$r(\mathbf{x})$を推測させる。
2. $r(\mathbf{x})$を用いて、上のImportance Weightingの式で最小化を行い、識別器を得る。

Test Domainが訓練するたびに変わってしまう状態について考える。

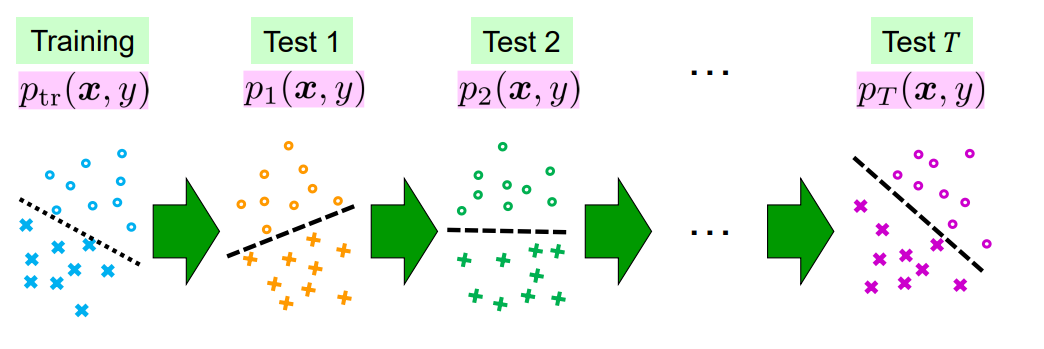
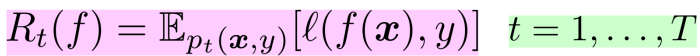
与えられるのは大量のラベル付けされた訓練データと、各TestでのDomainを代表する少量のUnlabaledデータ。

この問題設定では、各Test Domainに対してRetrainingが必要である。毎回やるのは効率が悪いので、Online Learningという手法を使う。

k_vol30-no5/

Online Convex Optimizationをする。凸関数の損失$l$があり、線形モデル$f(\mathbf{x}) = \mathbf{w ^ T x}$を考える。以下の式のように勾配法で更新するが、そのまま更新するのではなく、ある写像$\Pi _{\mathcal{W}}$を挟んでいる。